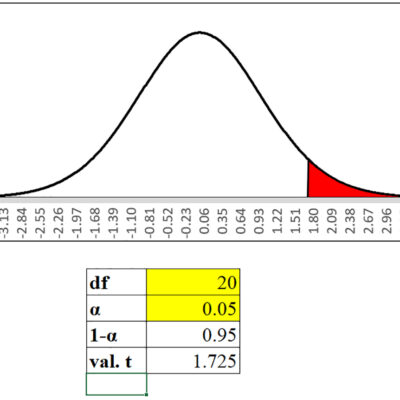
Mulți cercetători raportează acum cât de neobișnuit ar fi scorul t al eșantionului dacă ipoteza nulă ar fi adevărată, mai degrabă decât să aleagă un α și să afirme dacă scorul t al eșantionului implică faptul că datele susțin una sau alta dintre ipotezele bazate pe acel α. Când un cercetător face acest lucru, el lasă în esență cititorul raportului său să decidă cât de mult risc să-și asume pentru a face ce fel de greșeală. Există chiar și două moduri de a face acest lucru. Dacă vă uitați la o porțiune din orice tabel t de manual, veți vedea că nu este foarte bine configurat în acest scop; dacă doriți să puteți afla ce parte a unei distribuții t era peste orice scor t, ați avea nevoie de un tabel care să enumere mai multe scoruri t. Deoarece distribuția t variază ca df. modificări, chiar ați avea nevoie de o serie întreagă de tabele t, câte unul pentru fiecare df. Din fericire, șablonul interactiv Excel furnizat în Figura 5.1 vă va permite să aveți o imagine completă a tabelului t și a distribuției sale.
Modul de modă veche de a determina cititorul să decidă cât de mult din risc să-și asume este să nu menționați un α în corpul raportului dvs., ci doar să dați eșantionul de scor t în textul principal. Pentru a oferi cititorului câteva îndrumări, vă uitați la tabelul t obișnuit și găsiți cel mai mic α, să spunem că este 0,01, care are o valoare t mai mică decât cea pe care ați calculat-o pentru eșantion. Apoi scrieți o notă de subsol care spune: „Datele susțin ipoteza alternativă pentru orice α > 0,01.”
Modul mai modern folosește capacitatea unui computer de a stoca o mulțime de date. Multe pachete software statistice stochează un set de tabele t detaliate, iar atunci când se calculează un scor t, pachetul face computerul să caute exact ce proporție de eșantioane ar avea scoruri t mai mari decât cea pentru eșantionul tău. Tabelul 5.2 arată rezultatul computerului pentru problema lui LaTonya dintr-un pachet statistic tipic. Observați că programul obține același scor t ca și LaTonya, pur și simplu merge la mai multe zecimale. Observați, de asemenea, că arată ceva numit valoarea p. Valoarea p este proporția de scoruri t care sunt mai mari decât cel tocmai calculat. Privind la exemplu, statistica t calculată este 1,48 și valoarea p este 0,094. Aceasta înseamnă că, dacă există 6 df, puțin mai mult de 9% dintre eșantioane vor avea un scor t mai mare de 1,48. Amintiți-vă că LaTonya a folosit un α = 0,025 și a decis că datele acceptă Ho, valoarea p de 0,094 înseamnă că Ho ar fi acceptat pentru orice α mai mic de 0,094. Deoarece LaTonya a folosit α = 0,025, această valoare p înseamnă că nu găsește suport pentru Ho.
(Tabel. Rezultate din software-ul statistic tipic pentru problema lui LaTonya)
| Test de ipoteză: Medie |
| Ipoteza nulă: Medie = 11,71 USD |
| Alternativă: mai mare decât |
| Statistica t calculată = 1,48 |
| valoarea p = 0,094 |
Abordarea valorii p devine modalitatea preferată de a prezenta rezultatele cercetării către publicul cercetătorilor profesioniști. Majoritatea cercetărilor statistice efectuate pentru o firmă de afaceri vor fi utilizate direct pentru luarea deciziilor sau prezentate unui public de directori pentru a-i ajuta în luarea unei decizii. În general, aceste audiențe nu vor fi interesate să decidă singure care ipoteză susțin datele. Când faceți o prezentare a rezultatelor șefului dvs., veți dori să spuneți pur și simplu ce ipoteză susțin dovezile. Puteți decide folosind fie abordarea tradițională α, fie abordarea mai modernă a valorii p, dar a decide ce spun dovezile este probabil treaba dvs.
Sursa: Mohammad Mahbobi and Thomas K. Tiemann, Introductory Business Statistics with Interactive Spreadsheets – 1st Canadian Edition, © 2015 Mohammad Mahbobi, licența CC BY 4.0
© 2021 MultiMedia Publishing, Statistica pentru afaceri. Traducere și adaptare: Nicolae Sfetcu
Tehnologia Blockchain – Bitcoin
Internetul a schimbat complet lumea, cultura şi obiceiurile oamenilor. După o primă fază caracterizată prin transferul liber al informaţiilor, au apărut preocupările pentru siguranţa comunicaţiilor online şi confidenţialitatea utilizatorilor. Tehnologia blockchain asigură ambele aceste deziderate. Relativ nouă, ea are şansa să producă … Citeşte mai mult
Lucrul cu baze de date
Colecția ȘTIINȚA INFORMAȚIEI Lucrul cu bazele de date este astăzi printre cele mai căutate abilități IT. Acum puteți obține o bază de plecare în proiectarea și implementarea bazelor de date cu o abordare practică, ușor de înțeles. ”Lucrul cu baze … Citeşte mai mult
Introducere în inteligența artificială
Inteligența artificială s-a dezvoltat exploziv în ultimii ani, facilitând luarea deciziilor inteligente și automate în cadrul scenariilor de implementare. Inteligența artificială se referă la un ecosistem de modele și tehnologii pentru percepție, raționament, interacțiune și învățare. Asistăm la o convergență … Citeşte mai mult
Lasă un răspuns