Am văzut cum se calculează viteza medie între două poziții. Cu toate acestea, deoarece obiectele din lumea reală se mișcă continuu prin spațiu și timp, ne-am dori să găsim viteza unui obiect în orice punct. Putem găsi viteza obiectului oriunde de-a lungul traseului său folosind câteva principii fundamentale de calcul. Această secțiune ne oferă o perspectivă mai bună asupra fizicii mișcării și va fi utilă în capitolele ulterioare.
Viteza vectorială instantanee
Mărimea care ne spune cât de repede se mișcă un obiect oriunde de-a lungul traseului său este viteza instantanee, numită de obicei pur și simplu viteza. Este viteza medie între două puncte de pe traseu în limita în care timpul (și, prin urmare, deplasarea) dintre cele două puncte se apropie de zero. Pentru a ilustra matematic această idee, trebuie să exprimăm poziția x ca o funcție continuă a lui t notată cu x(t). Expresia pentru viteza medie între două puncte folosind această notație este = (x(t2) − x(t1))/(t2 − t1). Pentru a găsi viteza instantanee în orice poziție, lăsăm t1 = t și t2 = t + Δt. După introducerea acestor expresii în ecuația pentru viteza medie și luând limita ca Δt→0, găsim expresia pentru viteza instantanee:
v(t)=limΔt→0(x(t + Δt) − x(t))/Δt=dx(t)/dt.
| VITEZA INSTANTANEE
Viteza instantanee a unui obiect este limita vitezei medii pe măsură ce timpul scurs se apropie de zero sau derivata lui x în raport cu t: (3.4) v(t)=dx(t)/dt. |
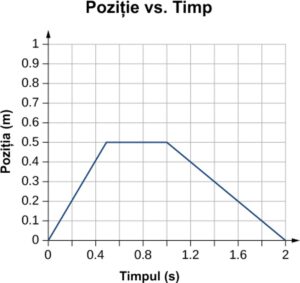
La fel ca viteza medie, viteza instantanee este un vector cu dimensiunea lungimii per timp. Viteza instantanee la un anumit punct de timp t0 este rata de schimbare a funcției de poziție, care este panta funcției de poziție x(t) la t0. Figura 3.6 arată cum viteza medie = Δx/Δt între momente de timp se apropie de viteza instantanee la t0. Viteza instantanee este afișată la momentul t0, care se întâmplă să fie la maximul funcției de poziție. Panta graficului de poziție este zero în acest punct și astfel viteza instantanee este zero. În alte momente, t1,t2 și așa mai departe, viteza instantanee nu este zero deoarece panta graficului de poziție ar putea fi pozitivă sau negativă. Dacă funcția de poziție ar avea un minim, panta graficului de poziție ar fi, de asemenea, zero, dând și acolo o viteză instantanee de zero. Astfel, zerourile funcției de viteză dau minimul și maximul funcției de poziție.
(Într-un grafic al poziției în funcție de timp, viteza instantanee este panta dreptei tangente într-un punct dat. Sunt prezentate vitezele medii = Δx/Δt = (xf – xi)/(tf – ti) între timpii Δt = t6 − t1, Δt = t5 − t2 și Δt = t4 − t3. Când Δt→0, viteza medie se apropie de viteza instantanee la t = t0.)
| EXEMPLUL 3.2
Găsirea vitezei dintr-un grafic poziție versus timp Având în vedere graficul poziție versus timp din Figura 3.7, găsiți graficul viteză versus timp.
Strategie Graficul conține trei linii drepte în trei intervale de timp. Găsim viteza în fiecare interval de timp luând panta dreptei folosind grila. Soluţie Interval de timp 0 s până la 0,5 s: = Δx/Δt = (0,5m − 0,0m)(0,5s − 0,0s) = 1,0 m/s Interval de timp 0,5 s la 1,0 s: = Δx/Δt = (0,5m − 0,5m)/(1,0s − 0,5s) = 0,0 m/s Interval de timp 1,0 s până la 2,0 s: =Δx/Δt = (0,0m − 0,5m)/(2,0s − 1,0s) = −0,5 m/s Graficul acestor valori ale vitezei în funcție de timp este prezentat în Figura 3.8.
Semnificaţia În intervalul de timp între 0 s și 0,5 s, poziția obiectului se îndepărtează de origine, iar curba poziție față de timp are o pantă pozitivă. În orice punct de-a lungul curbei în acest interval de timp, putem găsi viteza instantanee luând panta acesteia, care este de +1 m/s, așa cum se arată în Figura 3.8. În intervalul de timp următor, între 0,5 s și 1,0 s, poziția nu se schimbă și vedem că panta este zero. De la 1,0 s la 2,0 s, obiectul se deplasează înapoi spre origine și panta este -0,5 m/s. Obiectul are direcția inversă și are o viteză negativă. |
Viteza scalară
În limbajul de zi cu zi, majoritatea oamenilor folosesc termenii viteză (viteză scalară) și velocitate (viteza vectorială) în mod interschimbabil. În fizică, însă, ele nu au același sens și sunt concepte distincte. O diferență majoră este că viteza nu are direcție; adică viteza este un scalar. În limba română se obișnuiește să se dumească la fel ambii termeni, viteza, specificând în mod expres numele de viteza vectorială atunci când trebuie să se facă distincția între cei doi termeni.
Putem calcula viteza medie găsind distanța totală parcursă împărțită la timpul scurs:
(3.5) Viteza medie = = Distanța totală / Timp scurs.
Viteza scalară medie nu este neapărat aceeași cu mărimea vitezei vectoriale medii, care se găsește prin împărțirea mărimii deplasării totale la timpul scurs. De exemplu, dacă o călătorie începe și se termină în aceeași locație, deplasarea totală este zero și, prin urmare, viteza vectorială medie este zero. Viteza scalară medie, însă, nu este zero, deoarece distanța totală parcursă este mai mare decât zero. Dacă facem o călătorie de 300 km și trebuie să fim la destinație la o anumită oră, atunci ne-ar interesa viteza scalară medie.
Cu toate acestea, putem calcula viteza scalară instantanee din mărimea vitezei vectoriale instantanee:
3.6 Viteza instantanee = |v(t)|.
Dacă o particulă se mișcă de-a lungul axei x la +7,0 m/s și o altă particulă se mișcă de-a lungul aceleiași axe la -7,0 m/s, acestea au viteze vectoriale diferite, dar ambele au aceeași viteză scalară de 7,0 m/s. Unele viteze tipice sunt prezentate în tabelul următor.
| Viteza | m/s | mi/h |
| Deriva continentală | 10−7 | 2×10−7 |
| Mers vioi | 1.7 | 3.9 |
| Ciclist | 4.4 | 10 |
| Alergător de sprint | 12,2 | 27 |
| Limită de viteză în mediul rural | 24,6 | 56 |
| Record oficial de viteză pe uscat | 341,1 | 763 |
| Viteza sunetului la nivelul mării | 343 | 768 |
| Naveta spațială la reintrare | 7800 | 17.500 |
| Viteza de scăpare de gravitația Pământului* | 11.200 | 25.000 |
| Viteza orbitală a Pământului în jurul Soarelui | 29.783 | 66.623 |
| Viteza luminii în vid | 299.792.458 | 670.616.629 |
Tabelul 3.1 Vitezele diferitelor obiecte *Viteza de scăpare este viteza cu care un obiect trebuie să fie lansat astfel încât să învingă gravitația Pământului și să nu fie tras înapoi spre Pământ.
Calcularea vitezei vectoriale instantanee
Când se calculează viteza vectorială instantanee, trebuie să specificăm forma explicită a funcției de poziție x(t). Dacă fiecare termen din ecuația x(t) are forma Atn unde A este o constantă și n este un număr întreg, acesta poate fi diferențiat folosind regula puterii pentru ca fiind:
| (3.7) d(Atn)/dt=Antn−1. |
Rețineți că, dacă există termeni suplimentari adăugați împreună, această regulă de diferențiere a puterii poate fi făcută de mai multe ori și soluția este suma acelor termeni. Următorul exemplu ilustrează utilizarea ecuației 3.7.
| EXEMPLUL 3.3
Viteza instantanee versus viteza medie Poziția unei particule este dată de x(t) = 3,0t + 0,5t3 m. a. Folosind ecuația 3.4 și ecuația 3.7, găsiți viteza instantanee la t = 2,0 s. b. Calculați viteza medie între 1,0 s și 3,0 s. Strategie Ecuația 3.4 oferă viteza instantanee a particulei ca derivată a funcției de poziție. Privind forma funcției de poziție dată, vedem că este un polinom în t. Prin urmare, putem folosi ecuația 3.7, regula puterii din calcul, pentru a găsi soluția. Folosim ecuația 3.6 pentru a calcula viteza medie a particulei. Soluţie a. v(t) = dx(t)/dt = 3,0 + 1,5t2 m/s. Înlocuirea t = 2,0 s în această ecuație dă v(2,0s)=[3,0+1,5(2,0)2] m/s = 9,0 m/s. b. Pentru a determina viteza medie a particulei între 1,0 s și 3,0 s, calculăm valorile lui x(1,0 s) și x(3,0 s): x(1,0 s) = [(3,0)(1,0) + 0,5(1,0)3] m = 3,5 m x(3,0 s) = [(3,0)(3,0) + 0,5(3,0)3] m = 22,5 m. Atunci viteza medie este = (x(3,0 s) − x(1,0 s))/(t(3,0 s)−t(1,0 s)) = (22,5−3,5 m)/(3,0−1,0 s) = 9,5 m/s. Semnificaţie În limita în care intervalul de timp folosit pentru a calcula ajunge la zero, valoarea obținută pentru converge către valoarea lui v. |
| EXEMPLUL 3.4
Viteza vectorială instantanee versus viteza scalară Luați în considerare mișcarea unei particule în care poziția este x(t) = 3,0t − 3t2 m. a. Care este viteza instantanee la t = 0,25 s, t = 0,50 s și t = 1,0 s? b. Care este viteza particulei în aceste momente? Strategie Viteza vectorială instantanee este derivata funcției de poziție, iar viteza scalară este mărimea vitezei vectoriale instantanee. Folosim ecuația 3.4 și ecuația 3.7 pentru a rezolva viteza instantanee. Soluţie a. v(t) = dx(t)/dt = 3,0 − 6,0t m/s v(0,25 s) = 1,50 m/s, v(0,5 s) = 0 m/s, v(1,0 s) = −3,0 m/s b. Viteza scalară = |v(t)| = 1,50 m/s, 0,0 m/s și 3,0 m/s Semnificaţie Viteza particulei ne oferă informații despre direcție, indicând că particula se mișcă la stânga (vest) sau la dreapta (est). Viteza dă mărimea vitezei. Prin reprezentarea grafică a poziției, vitezei vectoriale și vitezei scalare în funcție de timp, putem înțelege vizual aceste concepte Figura 3.9. În (a), graficul arată particula care se mișcă în direcție pozitivă până la t = 0,5 s, când își inversează direcția. Inversarea direcției poate fi văzută și în (b) la 0,5 s, unde viteza vectorială este zero și apoi devine negativă. La 1,0 s este din nou la originea de unde a început. Viteza particulei la 1,0 s în (b) este negativă, deoarece se deplasează în direcția negativă. Dar în (c), totuși, viteza sa este pozitivă și rămâne pozitivă pe toată durata călătoriei. De asemenea, putem interpreta viteza ca panta graficului poziție față de timp. Panta lui x(t) scade spre zero, devenind zero la 0,5 s și din ce în ce mai negativă ulterior. Această analiză de comparare a graficelor de poziție, viteză vectorială și viteză scalară ajută la identificarea erorilor în calcule. Graficele trebuie să fie consecvente între ele și să ajute la interpretarea calculelor.
|
| VERIFICAȚI-VĂ ÎNȚELEGEREA 3.2
Poziția unui obiect în funcție de timp este x(t) = −3t2 m. (a) Care este viteza obiectului în funcție de timp? (b) Este viteza vreodată pozitivă? (c) Care sunt viteza vectorială și viteza scalară la t = 1,0 s? |
Sursa: Physics, University Physics (OpenStax), acces gratuit sub licență CC BY 4.0. Traducere și adaptare de Nicolae Sfetcu
© 2021 MultiMedia Publishing, Fizica, Volumul 1
Știința – Filosofia științei
Cartea explorează principalele teme și teorii ale științei și filozofiei contemporane a științei, evidențiind întrebările fascinante și provocatoare actuale din știință în generală și filosofia științei, cu accent pe metodele științifice. O mare parte din înțelegerea noastră provine din cercetarea … Citeşte mai mult
Singularitățile ca limite ontologice ale relativității generale
Singularitățile la care se ajunge în relativitatea generală prin rezolvarea ecuațiilor lui Einstein au fost și încă mai sunt subiectul a numeroase dezbateri științifice: Există sau nu, singularități? Big Bang a fost o singularitate inițială? Dacă singularitățile există, care este … Citeşte mai mult
Mecanica cuantică fenomenologică
O introducere la nivel fenomenologic, cu un aparat matematic minimal, în mecanica cuantică. Un ghid pentru cine dorește să înțeleagă cea mai modernă, mai complexă și mai neconformă disciplină fizică, un domeniu care a schimbat fundamental percepțiile oamenilor de știință … Citeşte mai mult
Lasă un răspuns