Distribuția F în statistică – Exemplu

Tânăra manager de bancă din exemplul anterior încă se luptă să găsească cea mai bună modalitate de a-și gestiona sucursala. Ea știe că trebuie să aibă mai mulți casieri vinerea decât în ​​alte zile, dar încearcă să afle dacă nevoia de casieri este constantă în restul săptămânii. Ea colectează date pentru numărul de tranzacții în fiecare zi timp de două luni. Iată datele ei:

Luni: 276, 323, 298, 256, 277, 309, 312, 265, 311

Marți: 243, 279, 301, 285, 274, 243, 228, 298, 255

Miercuri: 288, 292, 310, 267, 243, 293, 255, 273

Joi: 254, 279, 241, 227, 278, 276, 256, 262

Testează ipoteza nulă:

H₀ = m_m = m_tu = m_w = m_th

și decide să folosească α – 0,05. Ea descoperă:

m = 291,8

tu = 267,3

w = 277,6

th = 259,1

iar media mare = 274,3

Calculează variația din:

[(276 – 291,8)²+(323 – 291,8)² + … + (243 – 267,6)² + … + (288 – 277,6)² + … + (254 – 259,1)²]/[34 – 4] = 15887,6/30 = 529,6

Apoi calculează variația dintre:

[9(291,8 – 274,3)² + 9(267,3 – 274,3)² + 8(277,6 – 274,3)² + 8(259,1 – 274,3)²]/[4-1] = 5151,8/3 = 1717,3

Calculează scorul F:

F = 1717,3/529,6 = 3,24

Un element interactiv sau media a fost exclus din această versiune a textului. Îl puteți vizualiza online aici: https://www.telework.ro/wp-content/uploads/2022/02/Chapter-6_Fig-6.3_Analiza_ANOVA.xlsx

(Șablon Excel interactiv pentru ANOVA unidirecțional.)

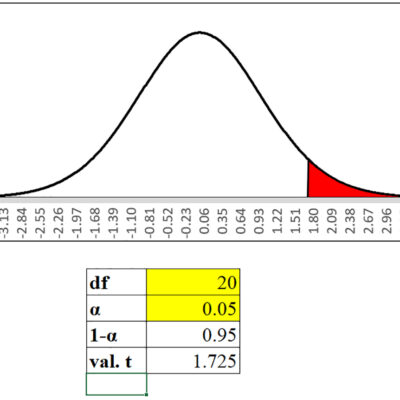
Puteți introduce numărul de tranzacții pentru fiecare zi în celulele galbene din Figura 6.3 și selectați α. După cum puteți vedea apoi în Figura 6.3, valoarea F calculată este 3,24, în timp ce tabelul F (F-Critic) pentru α – 0,05 și 3, 30 df, este 2,92. Deoarece scorul său F este mai mare decât valoarea F critică sau, alternativ, deoarece valoarea p (0,036) este mai mică decât α – 0,05, ea concluzionează că numărul mediu de tranzacții nu este egal în diferite zile ale săptămânii, sau măcar există o zi care este diferită de celelalte. Ea va dori să-și ajusteze personalul astfel încât să aibă mai mulți casieri în unele zile decât în ​​altele.

Rezumat

Distribuția F este distribuția de eșantionare a raportului dintre varianțele a două eșantioane extrase dintr-o populație normală. Este folosit[ direct pentru a testa dacă două eșantioane provin din populații cu aceeași varianță. Deși ocazional veți vedea că este folosit[ pentru a testa egalitatea varianțelor, cea mai importantă utilizare este în analiza varianței (ANOVA). ANOVA, cel puțin în forma sa cea mai simplă, așa cum este prezentată aici, este utilizată pentru a testa dacă trei sau mai multe eșantioane provin din populații cu aceeași medie. Testând pentru a vedea dacă varianța observațiilor provine mai mult din varianța fiecărei observații față de media eșantionului său sau din varianța mediilor eșantioanelor de la media mare, ANOVA testează pentru a vedea dacă eșantioanele provin din populații cu medii egale sau nu.

ANOVA are și forme mai elegante. Ea formează baza analizei de regresie, o tehnică statistică având multe aplicații de afaceri. Tabelele F sunt, de asemenea, folosite în testarea ipotezelor despre rezultatele regresiei.

Acesta este, de asemenea, începutul statisticii multivariate. Observați că în ANOVA unidirecțională, fiecare observație este pentru două variabile: variabila x și grupul din care face parte observația.

Testul F pentru egalitatea varianțelor este uneori folosit înainte de a utiliza testul t pentru egalitatea mediilor deoarece testul t, cel puțin în forma prezentată până acum, necesită ca eșantioanele să provină din populații cu varianțe egale. Veți vedea că este folosit împreună cu testele t atunci când valorile sunt mari sau cercetătorul este puțin compulsiv.

Sursa: Mohammad Mahbobi and Thomas K. Tiemann, Introductory Business Statistics with Interactive Spreadsheets – 1st Canadian Edition, © 2015 Mohammad Mahbobi, licența CC BY 4.0

© 2021 MultiMedia Publishing, Statistica pentru afaceri. Traducere și adaptare: Nicolae Sfetcu